Turn rate und Turn radius Berechnung
Table of Contents
Um was geht es uns?
Viele Formelsammlungen und RoT (Rule of Thumbs) weisen unzählige Formeln aus.
Alle etwas haben etwas gemeinsam: Sie stellen eine Näherung für den alltäglichen Gebrauch dar.
Hier die „best of“:
Turn rate für Standard Rate ist 3° pro Sekunde, daher:
AOB= TAS/10 + 7
(z.B. TAS 120/10 +7 => 19° AOB für Standard rate turn)
Turn radius für einen mit Standard rate ausgeführte Kurve:
TAS/100
(z.B. 120Kts/100 => 1,2NM)
Mx10 – 2
(z.B. M0.7 – 2 => 5NM)
Dieser Ansatz ist schon komplexer:
V2 /sin AOB/g = Kreisdurchmesser in Meter
Falls also Radius gewünscht, noch durch 2 teilen, in KM und dann in NM umformen (durch 1,85 teilen)
(z.B. 1202 / sin 19° / 9,81 m/sec => 4508,70m (:1000) (:2) (:1,85) =>1,22NM
Umdrehen im Tal? Oder nicht?
Was aber mit einer Frage wie:
Wieviel Platz benötige ich, wenn ich in einem Tal mit 120 KIAS und 45° AOB notfallmäßig umdrehen möchte?
Dann stoßen alle diese Formeln an ihre Grenzen. Zudem findet nie eine höhere Turn rate Beachtung, auch Wind wird nie beachtet um ggf. den Groundtrack abzubilden. Und was ist mit den G’s?
Also dann doch mal von vorne:
Definition Turn rate:
Die Richtungsänderung des Flugvektors in Grad/ Sekunde.
Definition Turn radius:
Der Radius der Kurve, der durch den Flugvektor beschrieben wird. Üblicherweise in NM angeben.
Wir betrachten die Kurve mal anders:
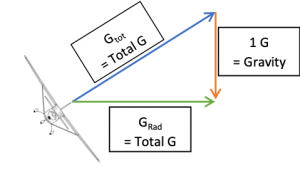
Die Beschleunigung als Gtot bezeichnet, ist der am G-Meter (falls vorhanden) angezeigte Wert
Um einen Höhenverlust/ -gewinn in der Kurve zu vermeiden muss der Vektor, der der Erdanziehung (Gravity) entgegengesetzte ist, genau 1G betragen. Daraus resultierend ist nun Grad (= Turn Radius)
Erst mal was bekanntes aus dem rechtwinkligen Dreieck:
Gtot= 1/ cos AOB
Je größer der AOB, desto mehr Gtot entstehen bei einem Kurvenflug
Grad= Gtot x sinAOB
Je größer die Gtot sind, umso größer ist Grad (= Zentripetalkraft)
Ist einleuchtend. Für Steig-/ bzw. Sinkflüge bitte unter Specific excess power nachsehen.
Ergibt sich also nun für den Turn radius (Ergebnis in ft):
r= v2/(GRad x g)
(v in ft/sec; und g =32,18 ft/sec2
Und für die Turn rate °/ sec:
Turn rate= (g x GRad x K)/ v
(K= 57,3° vom Bogenmaß abgeleitet), wiederum g = 32,18 ft/sec2 )
Das Ergebnis
Wie aus den Formeln ersichtlich, ist für einen engen Turn radius eine geringe Geschwindigkeit (da sie im Quadrat eingeht) und hohe GRad vorteilhaft.
Für eine hohe Turn rate ist eine hohe GRad optimal (also respektive hohe Gtot) und das bei einer möglichst geringen Geschwindigkeit.
Wie man diese Variablen beeinflussen kann, gerne unter Specific excess power.
Sich einmal die Zeit nehmen und sich wirklich mal Gedanken machen, was mein Flugzeug kann, am besten bei 60 Kts GS rentiert sich wirklich. Man hat dann mehr Argumentationsmöglichkeiten , wenn mal irgendwelche „Weisheiten“ am Fliegerstammtisch zum Besten gegeben werden. Zudem wird jeder überrascht sein, wie klein der Turn radius in Wirklichkeit ist!
Wer nicht so gerne rechnet, hier in Link, der alle Werte „ausspuckt“:
0 Kommentare